Генеральная совокупность – определение, использование, расчёт

Генеральной совокупностью называется набор всех объектов или единиц, относительно которых будут делаться выводы в рамках конкретного исследования. Если сильно упростить, то для маркетолога это его целевая аудитория.

Тут важно заметить, что от правильного определения генеральной совокупности будет напрямую зависеть количество анкет, достаточных для адекватных выводов и аналитики. А теперь давайте как можно глубже погрузимся в определения, статистику и механику расчётов.

Что такое генеральная совокупность – определение

Слово «генеральная» происходит от латинского generalis, что означает «общий» или «родовой». Однако в английском используется альтернативный термин – population (русск. «популяция»), вместо general (хотя это слово происходит от того же generalis). Соответственно…

Генеральная совокупность – это общая или максимально полная группа объектов, людей, событий или явлений, обладающих определёнными характеристиками и подлежащих изучению в рамках конкретного статистического исследования. Выводы, сделанные по итогам анализа, будут актуальны для всей этой совокупности.

Читайте также: Какие методы исследования бывают.

Ключевые характеристики генеральной совокупности

• Полнота охвата. Совокупность должна охватывать абсолютно все объекты, соответствующие заданным критериям.
• Определённость. Когда чётко заданы критерии включения объектов в совокупность – их характеристики, параметры отбора, триггеры и пр.
• Цель исследования. Для совокупности определены состав, границы и задачи.
• Размер. Он может быть конечным (например, все ученики конкретной школы) или бесконечным (когда точный размер совокупности определить невозможно или он постоянно меняется).

Виды генеральной совокупности

Варианты генеральной совокупности можно классифицировать по разным критериям. Например:

1. По объёму (количеству элементов)

• Конечная или реальная — имеет чётко определённое число объектов, которое можно подсчитать. Например: все студенты конкретного ВУЗа в 2026 году, все домохозяйства в определённом микрорайоне города.
• Гипотетическая — имеет теоретически неограниченное число элементов. Часто встречается в математической статистике и при моделировании. Например: все возможные результаты бросков монеты, все измерения температуры воздуха в определённой точке за бесконечный период.

2. По степени однородности

• Гомогенная (однородная) — включает объекты, которые обладают схожими характеристиками и признаки. Анализ такой совокупности значительно проще, так как требуется меньшая выборка для репрезентативности. Например: партия одинаковых лампочек одного производителя, группа людей одного возраста и профессии.
• Гетерогенная (неоднородная) — включает подгруппы объектов с разными свойствами. Из-за чего требует более сложного подхода к выборке, таких как стратификация. Примеры: всё население города (здесь внутри будут разные возрасты, профессии, доходы), все предприятия региона (малые, средние, крупные, из разных отраслей).

Читайте также: Как найти статистические отклонения (выбросы) в опросах

3. По структуре (внутреннему делению)

• Простая (неструктурированная) — когда совокупность не делится на значимые подгруппы по целям исследования. Например: набор одинаковых деталей с конвейера.
• Структурированная (стратифицированная) — совокупность состоит из чётко выделенных слоёв (страт), различающихся по ключевым признакам. Их можно и нужно учитывать при формировании итоговой выборки. Например: население страны по регионам, студенты ВУЗа по факультетам, клиенты банка по уровню дохода.

4. По динамике

• Статичная (фиксированная) — состав совокупности не меняется за время проведения исследования. Например: жители дома на момент переписи, книги в библиотеке на конкретную дату.
• Динамическая (текущая) — состав может меняться: элементы добавляются или исключаются за время исследования. Например: клиенты онлайн‑сервиса (регистрируются/уходят), пациенты поликлиники (поступают/выписываются), товары на складе (поступают/продаются).

5. По типу элементов

• Количественная — объекты характеризуются измеримыми числовыми параметрами. Например: рост людей, вес продукции, температура воздуха.
• Качественная — объекты группируются по категориям и признакам без числовой шкалы. Например: виды растений в лесу, типы профессий, предпочтения брендов.
• Смешанная — содержит и количественные, и качественные признаки. Например: анкета, где есть возраст (число) и любимый цвет (категория).

Использование генеральной совокупности в статистических исследованиях

Генеральная совокупность применяется в исследованиях для разных сфер и бизнеса:

• В маркетинге и социологии – для определения целевой аудитории, оценки продукта и спроса на него, анализа предпочтений и т.п.
• В экономике и финансах – для мониторинга и прогнозирования рыночных показателей, изучения социальных групп и слоёв населения.
• На производстве – для проверки качества продукции (при выявлении ошибок и дефектов) и соответствия установленным стандартам, для оптимизации рабочих процессов и пр.

Обратите внимание! Вся генеральная совокупность очень редко участвует в исследованиях, так как это слишком затратно и долго. Но именно на основе генеральной совокупности определяется база и правила для наиболее репрезентативной выборки, а также формулируются параметры для последующего сравнения результатов: средние значения, дисперсия и т. п.

Преимущества использования генеральной совокупности при проведении исследований можно перечислить так:

1. Повышение точности и ценности данных – благодаря правильному охвату выборки.
2. Обеспечение достаточной полноты – на основе полных данных проще делать адекватные выводы и искать закономерности.
3. Юридическая значимость – выводы полноценных исследований, проведённых по всем правилам, могут являться официальным источником информации для принятия важных управленческих решений, в том числе в госструктурах.

Чем отличаются генеральная и выборочная совокупность

Как можно догадаться из формулировки терминов:

Генеральная совокупность — это ВСЯ совокупность объектов или наблюдений, к которым относятся выводы исследования. Точность исследования по генеральной совокупности является абсолютной – она охватывает все возможные варианты и отклонения.

А выборочная совокупность — это уже ЧАСТЬ генеральной совокупности, отобранная по определённым правилам, которые соотносятся с исходными целями исследования. Выборочная совокупность сохраняет те же свойства, что и генеральная, поэтому позволяет уменьшить объём исследования. В связи с этим ключевое требование к выборочной совокупности — репрезентативность, то есть способность корректно отражать свойства всей генеральной совокупности. Исследование по выборочной совокупности не может быть абсолютно точным, здесь всегда будут отклонения и погрешности.

Как определить или рассчитать генеральную совокупность

На всякий случай уточним – генеральная совокупность не рассчитывается, для неё нет формул. Она задаётся. Именно она выступает базой для всех последующих действий с выборкой. Чтобы лучше понять процесс, давайте разберёмся с ним пошагово.

Шаг 1. Определяем границы генеральной совокупности

Полный список объектов исследования будет напрямую соотноситься с целями и задачами этого исследования. Поэтому вам нужно определиться с тем, что и где вы будете выяснять, на какие вопросы искать ответы и в какой среде. Для этого нужно использовать критерии включения в совокупность. В роли критериев могут выступать:

• Географические признаки (где живёт потенциальная аудитория).
• Демографические параметры (пол, возраст, социальный статус и пр.).
• Поведенческие факторы и триггеры (на основе активности целевой группы).
• Временные рамки. Обычно данные берут за какой-то период – год, месяц, квартал, неделя, день. Можно также задействовать связь с определённым событием. Благодаря привязке ко времени, итоги исследования удобно сравнивать за разные периоды.
• Любые другие критерии и свойства, например, профессиональные навыки, наличие автомобиля, стаж, квалификация и пр.

Если критерии получаются слишком общими, то можно пойти от обратного и задать исключения – какие группы объектов НЕ стоит включать в совокупность. Тот же подход можно использовать и для уточнения деталей вашей выборки.

Шаг 2. Считаем (задаём) объём генеральной совокупности (N)

Тут могут быть разные подходы. Но чаще всего для расчёта используются:

• Данные прямого учёта. Например, списочная численность сотрудников.
• Данные из официальных источников статистики. Например, информация из переписи населения для конкретного города или субъекта.
• Оценки экспертов и исследования рынка. Обычно это примерные показатели, которые эксперты предполагают или моделируют на основе своего опыта. Их можно уточнить за счёт сравнения с мнениями и оценками других экспертов из той же отрасли.
• Данные из технических систем. Например, из CRM, систем-аналитики, датчиков для подсчёта посетителей и пр.

Объём генеральной совокупности – это полное число всех элементов и объектов, которые подходят под обозначенные цели исследования и критерии отбора. Например, ВСЁ население города или ВСЕ работники предприятия.

На этом работа с генеральной совокупностью закончена. Но для полноценного исследования потребуются следующие шаги.

Шаг 3. Расчёт объёма выборки (n)

Выборка – это небольшая часть генеральной совокупности, которая сохраняет все основные её свойства с небольшой (допустимой) погрешностью и отклонениями.

Объём выборки может рассчитываться по разным формулам – тут всё будет зависеть от равномерности распределения нужных признаков или характеристик объектов, а также от требуемой нам точности исследования.

Наиболее распространённые формулы расчёта – для случайных величин:

1. Если генеральная совокупность существенно больше предполагаемой выборки, например, размер потенциальной аудитории более 100 тыс. человек, то применяется формула вычисления доли:

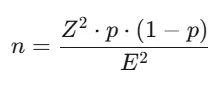
2. Если выборка сопоставима с генеральной совокупностью или объём совокупности конечный, то применяется специальная поправка:

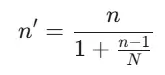
Альтернативный вариант той же формулы:

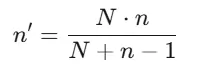
n – это наша искомая выборка,

n’ – скорректированная выборка на основе конечной генеральной совокупности,

Z – это коэффициент доверия (он зависит от доверительной вероятности),

p – это ожидаемая доля выбранного признака,

E – допустимая ошибка выборки.

Пока всё очень запутано, поэтому давайте посчитаем более предметно.

Пример расчёта выборки для опроса всех сотрудников компании по результатам корпоративного обучения

Предположим, что нам нужно выяснить, кто остался доволен обучением, а кто нет. Пусть генеральная совокупность равна 3500 человек – это списочная численность тех, кто прошёл обучение. Другие вводные: p=0,5 (для максимального объёма выборки, когда ожидаемая доля признака стремится к половине всей совокупности), ошибка – не более 4% (E=0,04), а доверие – 95% (это «золотой стандарт» для маркетинговых исследований, в этом случае значение Z известно заранее – 1,96; если нужно доверие до 99%, то Z будет примерно 2,58).

1. Сначала считаем по формуле доли для бесконечной совокупности:

n = (1,96² * 0,5 * 0,5) / 0,04² ≈ (3,8416 * 0,25) / 0,0016 = 600,25

Получается, что нам нужно опросить не менее 601 сотрудника (округлили в большую сторону).

2. Уточняем выборку на основе «конечности» генеральной совокупности:

n' = 601 / (1+(601-1)/3500) ≈ 601 / 1,17142 = 513,13

На всякий случай округлим в большую сторону, тогда получается, что нам нужно опросить около 514 работников, чтобы получить репрезентативную выборку.

Всё, можно приступать к исследованию. Сотрудников для опроса нужно выбирать случайным образом – из разных отделов, с разным стажем, полом, возрастом и пр.

Читайте также: Как работает модель Киркпатрика? Разбираем 4 уровня оценки эффективности обучения.

Шаг 4. Проверка достоверности результатов

Это самый важный и ответственный шаг, о котором многие маркетологи забывают. Предположим, что мы провели своё исследование на основе опроса 514 респондентов. И выяснилось, что доля довольных обучением составила 68%, хотя мы предполагали 50% (p=0,5).

Считаем доверительный интервал с фактически достигнутой точностью. Начинаем со стандартной ошибки доли:

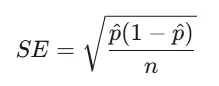
SE = √(0,68*(1-0,68)/514) ≈ 0,02057

Тогда предельная погрешность будет равна:

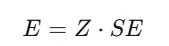
E = 1,96 * 0,02057 ≈ 0,04032

Осталось посчитать доверительный интервал (от… и до…):

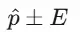
• Нижняя граница: 0,68 − 0,04032 = 0,63968
• Верхняя граница: 0,68 + 0,04032 = 0,72032

То есть, с вероятностью 95 % истинная доля в генеральной совокупности лежит в интервале 63,97% - 72,03%. Фактически достигнутая точность исследования: ± 4,03%.

Важные заключительные мысли по генеральной совокупности

Основная проблема статистики сводится к тому, что выборка почти никогда не является идеально уменьшенной копией генеральной совокупности. Она почти всегда искажает её свойства. Вот прям наверняка! Поэтому критически важно, чтобы выборка была репрезентативной (то есть она должна действительно отражать и максимально полно воспроизводить параметры генеральной совокупности), а также по-настоящему случайной (когда каждая единица генеральной совокупности имеет известную, желательно равную, вероятность попасть в выборку).

Если вы не доверяете «случайностям», то можно пойти от обратного. Провести пилотное исследование на небольшой группе, выявить внутренние подгруппы и критерии, а затем масштабировать модель на вашу выборочную совокупность. То есть касательно нашего примера, вместо случайных 514 респондентов будут выбираться те, кто подходят под определённые критерии: имеют нужный пол и возраст, стаж, квалификацию, работают в конкретных отделах и пр. Ключевая идея – такая выборка будет пропорционально уменьшенной копией всего предприятия.

Если выборка не репрезентативна, то есть смещена на одну из ключевых характеристик / параметров исследования, то выводы о генеральной совокупности будут неверными, даже при достаточно большом объёме выборки.

Простой пример: опрос о том, довольны клиенты качеством товара, только среди тех, кто обращается в службу поддержки с проблемой (поломка, возврат, брак и т.п.).

Смотрите также: Как респонденты искажают свои ответы, подробный разбор