Как найти статистические отклонения (выбросы) в опросах

Статистические всплески (отклонения от стандартного ряда) могут либо указать на аспекты, о которых вы могли даже не догадываться перед запуском опроса, либо существенно исказить результаты исследования и привести к неправильным выводам.

Чтобы быть во всеоружии, нужно привлечь на свою сторону математику, в частности проверенные временем статистические методы и подходы. О них и пойдёт речь в этом материале – научим вас определять врут ли ваши опросы или нет.

Какие существуют методы выявления ошибок и отклонений в результатах опросов

Результаты опросов практически никогда не бывают идеально «чистыми» и достоверными: респонденты могут отвечать невнимательно, выбирать варианты механически, пропускать отдельные вопросы, давать заведомо неверные ответы или намеренно искажать данные.

Более того, ошибки могут возникать и на уровне процесса сбора информации: из-за неверной логики анкеты, технических сбоев, дублирования записей и т.п. Самый первый признак того, что что-то пошло не так – появление неожиданных выбросов (всплесков) и статистических отклонений. Они явным образом выбиваются из общей картины.

Для обнаружения отклонений от стандартных статистических рядов применяются разные подходы. Их условно можно разбить на следующие группы:

1. Визуальные методы. Позволяют быстро оценить распределение данных и своими глазами увидеть аномальные точки без сложных расчётов (или по их итогам). Они удобны при первичном анализе для любых типов выборок, а также при создании результатирующих отчётов по окончанию исследования. Примеры визуализации опросов и данных исследований: гистограммы, карты распределения плотности, диаграммы размаха (boxplot) и т.п.
2. Пороговые методы. Основаны на определении неких пороговых значений – «нормальных» пределов от… и до… Допустимые диапазоны значений задаются заранее. Например, возраст респондента 18-99 лет, допустимое время прохождения анкеты не более 5 минут. Если ответ отличается от заданного порога, то он сразу попадает в категорию невозможных или подозрительных. Примеры: фильтрация по диапазону, удаление очевидных ошибок ввода (ответы вида «йцук» или «фыва»), контроль времени прохождения.
3. Статистические методы. Могут быть относительно простыми и предельно сложными, всё будет зависеть от выбранной математической модели. В основе всегда числовые характеристики выборки: средние значения, медианы, мера разброса и т.п. Статистические методы позволяют объективно оценить, насколько отдельные ответы отличаются от типичной картины, основанной на результатах одного или сразу нескольких опросов. Примеры: Z-оценка, модифицированная Z-оценка (MAD), межквартильный размах (IQR), квартили.
4. Модельные методы и методы на основе машинного-обучения (ML). Это уже «высший пилотаж» с привлечением искусственного интеллекта или особой математической модели. Выбросы (всплески) определяются на основе разных паттернов ответов. Модели будут полезны при больших массивах данных или в случае использования сложных анкет. Примеры: кластеризация ответов, «Изолирующий лес» (Isolation Forest), локальный фактор выбросов (LOF).

Выбор подхода всегда определяется его сложностью, необходимостью применения профильного программного обеспечения (как альтернатива – облачных сервисов), совместимостью с результатирующими данными (а они в свою очередь зависят от типов вопросов и дополнительных данных об ответах/респондентах).

Ниже мы подобрали наиболее универсальные подходы, которые обеспечивают достаточную наглядность и достоверность, простоту расчётов, не требуют использования специальных программ. Это:

• Z-оценка (Z-score), а для некоторых случаев – модифицированная Z-оценка (MAD, Median Absolute Deviation).
• Межквартильный размах (IQR-rule / правило 1.5·IQR).
• Диаграмма размаха (Boxplot).
• Простая сортировка и просмотр крайних значений (экстремумов – минимума и максимума).

О них и расскажем поподробнее ниже – от простого к сложному.

Сортировка и просмотр крайних значений

Самый элементарный вариант без сложных математических моделей. При анализе результатов опроса следует отсортировать ответы по значениям и детально изучить те, которые относятся или близки к минимальным, а также к максимальным.

Например, если речь о произвольных ответах (для открытых вопросов), то числовым показателем может выступить длина текста в символах. То есть вам нужно предельно осторожно и вдумчиво изучить самые короткие и самые длинные ответы – они точно будут выбиваться из общей картины.

Если речь об оценке, например, в NPS-опросах или в CSat, то вам нужно изучить ответы с низкими и с максимальными значениями (хотя, тут по логике вещей наиболее информативными будут ответы с низкой оценкой – от критиков/недовольных клиентов).

Стандартизированная оценка (Z-оценка)

Суть метода можно описать так: Z-оценка показывает, насколько конкретное значение ответа отклоняется от среднего значения в единицах стандартного отклонения. Это классический метод для выявления аномальных значений в больших выборках, распределённых близко к нормальному.

Формула:

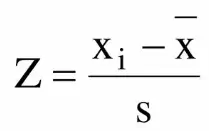
Здесь:

• x_i – это выбранное значение,
• x – это среднее арифметическое,
• S – стандартное отклонение.

При анализе результатов опросов Z-оценка хорошо подходит для:

• числовых шкал (например, оценка 1–10),
• времени ответа,
• количества выбранных пунктов.

Не стоит применять там, где присутствуют сильно скошенные распределения.

Пример расчёта

Допустим, респонденты оценивали удовлетворённость по шкале от 1 до 10. Среднее значение получилось 6, а стандартное отклонение – 2,345.

При ответе респондента, равном 10, Z-значение будет иметь вид:

Z = (10 – 6) / 2,345 ≈ -1,706

Если порог выбросов установлен на модуль числа Z > 3, то значение –1,706 считается статистически нормальным.

Как считается стандартное отклонение (в нашем случае оно выборочное, так как опрос проводится не по всей аудитории, а только по её части), формула:

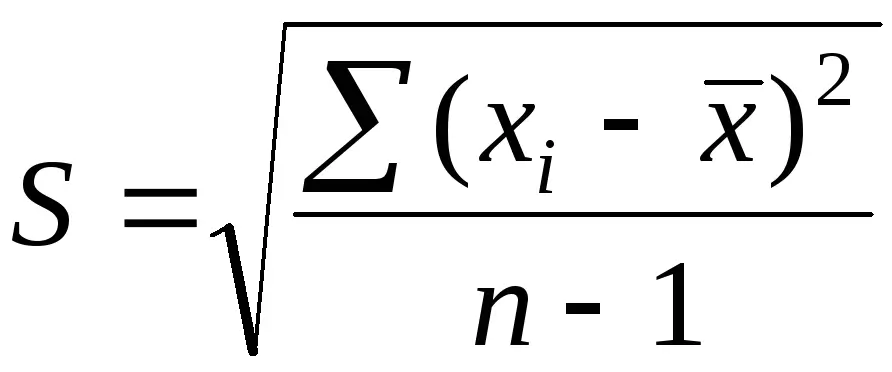
Здесь:

• x_i – это выбранное значение,
• x – это среднее арифметическое,
• n-1 – это коррекция Бесселя, а n – это количество наблюдений (число анкет или ответов).

Пример расчёта для ряда значений: 4, 5, 6, 5, 10.

• Среднее арифметическое = (4+5+6+5+10)/5 = 6.
• Коррекция Бесселя = 5-1 = 4.
• Сумма квадратов для всего ряда = (4-6)²+(5-6)²+(6-6)²+(5-6)²+(10-6)² = 4+1+0+1+16 = 22.
• Стандартное отклонение = √(22/4) ≈ 2,345.

Модифицированная Z-оценка на основе MAD

В отличие от исходного метода использует медианное абсолютное отклонение (MAD), а не стандартное. Это делает метод более устойчивым к серьёзно искажённым данным и сильной асимметрии.

Формула:

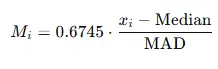
Здесь:

• 0,6745 – это нормирующий множитель, который является значением 75-го процентиля (квартиля) для стандартного нормального распределения,
• x_i – это выбранное значение,
• Median – медианное значение,
• MAD – медиана абсолютных отклонений (относительно основной медианы).

Считаем всплески на том же ряду значений: 4, 5, 6, 5, 10.

• Сначала упорядочиваем ряд: 4, 5, 5, 6, 10. В середине 5, это и есть медиана (если бы было сразу 2 значения для чётного числа значений, то посчитали бы как арифметическое среднее между двумя числами в середине).
• Абсолютные отклонения для медианы: 5-4=1, 5-5=0, 6-5=1, 5-5=0, 10-5=5.
• Упорядочиваем – 0, 0, 1, 1, 5. Медиана – 1 (это и есть MAD).
• Модифицированная Z-оценка для значения 10 = 0,6745 * (10-5)/1 = 3,3725.

Порог всплесков иногда устанавливается 3, а иногда 3,5. Для первого случая оценку на 10 баллов можно назвать отклонением от нормы. Но при значении порога в 3,5 она отклонением не является.

Межквартильный размах (IQR-rule / правило 1.5·IQR)

Суть метода сводится к тому, что под всплесками (отклонениями от нормы) понимаются все значения случайной величины, которые выходят за пределы в 1,5 квартиля по краям от межквартильного размаха (для лучшего понимания изучите картинку ниже). Это чем-то напоминает первый подход – с максимумом и минимумом, но только с привлечением сильных статистических методов.

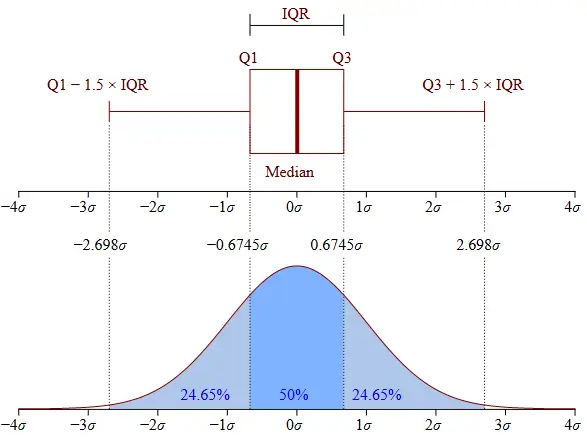
Квартиль – это общее обозначение диапазонов значений, которое соответствует доле 25% от всех значений, которые можно встретить в выборке.

Всего квартилей три: нижний (он же первый) – соответствует 25 процентилю (то есть охватывает первые 25% всех значений выборки), второй (медианный) – 50 процентиль (50% от всех значений выборки), верхний (третий) – 75 процентиль (75% от всех значений выборки).

Все значения, которые попадают в диапазон между первым и последним квартилем можно смело назвать нормальными. Это и есть межквартильный размах (IQR).

Всё, что не попадает в IQR – это всплески или отклонения.

Правило 1,5·IQR ещё больше смещает границы медианы, чтобы наверняка отсечь наиболее сильные отклонения.

Пример расчёта

Предположим, что респонденты поставили следующие оценки в опросе: 9, 4, 5, 5, 6, 6, 6, 7.

Сортируем по возрастанию и определяем медиану – 4, 5, 5, 6, 6, 6, 7, 9. Наше медианное значение – 6 (у нас в середине две шестёрки, среднее арифметическое для них – (6+6)/2=6). Она условно разделяет ряд значений пополам.

Q2 = 6

В первой половине ищем свою медиану – 4, 5, 5, 6. Тут медиана – 5 (считаем как (5+5)/2=5). Это наш первый квартиль.

Q1 = 5

Теперь медиана для второй половины: 6, 6, 7, 9. Она будет равна (6+7)/2 = 6,5.

Q3 = 6,5

Считаем межквартильный интервал:

IQR = Q3-Q1 = 6,5-5 = 1,5

Теперь определяем границы по 1,5 IQR сверху и снизу:

• Снизу: Q1 - 1,5 IQR = 5-1,5*1,5 = 2,75
• Сверху: Q3 + 1,5 IQR = 6,5+1,5*1,5 = 8,75

Теперь мы легко можем определить всплески – это всё, что меньше 2,75 (таких значений в ответах нет) и больше 8,75 (в нашем случае есть один ответ – на 9).

Согласитесь? Достаточно сложно для восприятия.

Диаграмма размаха (Boxplot) как инструмент визуализации отклонений выбросов

Ящик с усами, усиковая диаграмма, блочная или коробочная диаграмма – как её только не называют. Суть остаётся одной – визуализировать межквартильные размахи. Схематическое отображение правила 1,5·IQR чем-то напоминает японские свечи для биржевых графиков, но смысл отличается.

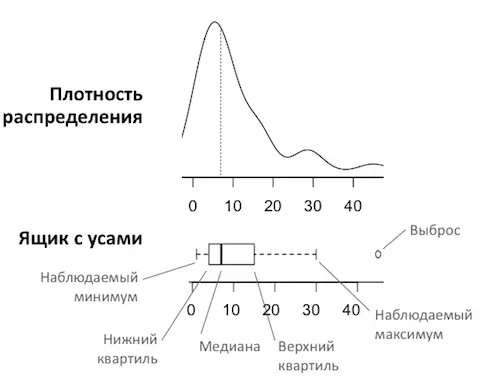
Как читать «ящик с усами»:

• Основная «коробка» – это область между границами квартилей, между первым и третьим (тот самый межквартильный интервал, IQR).
• Разделитель внутри «коробки» – медиана (второй квартиль).
• «Усы» – это наблюдаемый минимум и максимум. Если визуализация происходит по правилу 1,5 IQR, то это границы Q1 – 1,5*IQR и Q3 + 1,5*IQR.
• Если точка конкретного значения не попадает в область коробки с усами, то это выброс (отклонение).

Дополнительная картинка для лучшего понимания.

С помощью Boxplot-диаграмм легко можно визуализировать большой список значений и отклонений к ним. То есть вы сможете оценить выбросы не для одного конкретного вопроса в исследовании, а для всех вопросов сразу.

Например, вы можете построить диаграмму для респондентов по времени прохождения опроса у разных возрастных категорий. Все точки, которые будут за пределами «усов» – это ваши девиации (те, кто проходил опрос слишком быстро или слишком медленно).

Заключение и рекомендации

Ради справедливости стоит сказать, что ни один из математических подходов не даст вам 100% гарантий того, что вы обнаружили явную ошибку или проблему, и её можно смело удалять из выборки. Каждый отдельный случай отклонения следует рассматривать индивидуально. С определённой долей вероятности могли ошибиться вы сами (при составлении анкеты), а может и конкретное отклонение на поверку окажется вполне реальным (так тоже бывает).

Единственное, что делает математика – помогает с выявлением значений, которые отличаются от других.

Мы привели лишь наиболее простые и понятные подходы, но в своих исследованиях вы можете подключить и более «тяжёлые» математические модели.

Какой бы сложной ни была анкета, вам потребуется удобный инструмент для создания опроса и сбора данных. Выбирайте WebAsk!